In geophysical applications one has large data sets, i.e. 10,000 to 1 million data points, with a very irregular sampling geometries. For visualization or further data processing one needs data on a regular grid. Thus the problem is to interpolate or approximate the measurements onto the grid in an efficient way. This can be done by fast and robust algorithms and taking additional information concerning the statistical properties or the underlying physical process into account.
To get an overview of the concept, consider the following examples:
Gravity measurements in the Neusiedlersee area
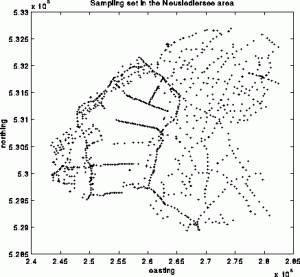
This is a typical example of a geophysical sampling set. The data are gravity measurements from the Neusiedlersee region in the eastern part of Austria. The so-called Bouguer anomaly measurements were made during a cold winter when the lake was completely frozen, allowing the researchers to gather data on the otherwise unaccessible interior of the lake. These samples cause the line-type features in the sampling set. The number of samples is 989.
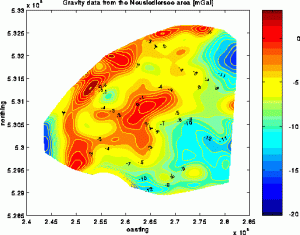
Here you see a contour plot of the reconstruction of the Bouguer anomaly with a two dimensional version of the ACT-method, developed at NUHAG. The original algorithm has been adapted to the geophysical setup. It involves a weight function which resembles the shape of the gravitational potential in the frequency domain. The incooperation of the knowledge of the underlying physical process leads to a stable version of the algorithm especially suited for the smooth approximation of data from potential functions.
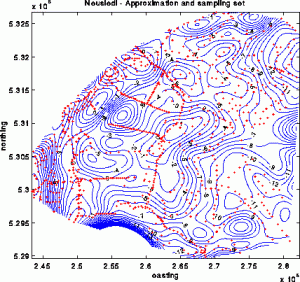
In order to obtain a better overview of the approximation an overlay of the sampling set and the contour map is shown here. The strong negative anomalies on the southern and eastern boundary of the region are very probably spurious features arising from the periodicity of the solution computed with ACT. This is not really a drawback as the most interesting parts of a survey are in practice always near the center of the region under consideration.
Airborne magnetics in the Bad Gleichenberg area
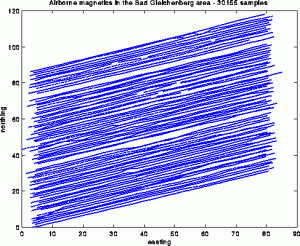
This is a typical example of a sampling set arising in airborne geophysics. In Austria these airborne survey are carried out with a helicopter that is equipped with a variety of measuring devices. This results in so-called line-type sampling geometries, which are characterized by a very high sampling density along the profiles and no data between the lines of flight, therefor having a strong spatial anisotropy in the data density.
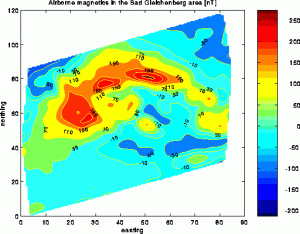
This is not only the most difficult sampling geometry but also a very common one, as airborne surveys allow to gather a huge amount of data in a very short time. In this example here we have more than 30000 sampling points.
In this image here, you see the contour map of an anomaly of the total intensity of the earth’s magnetic field. The gridding has been done with the ACT algorithm.
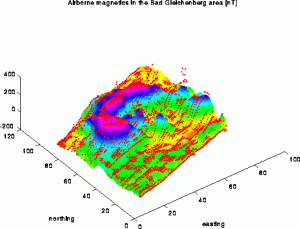
Magnetic measurements are very sensitive to noise. Especially human artifacts, such as cars, power-lines, etc. cause small scale anomalies with a high magnitude. A good gridding algorithm should therefor not try to fit the data exactly but rather the error envelope of the measurements. You can see in this figure, which is an overlay of a 3D view of the anomaly and the sampling set, that the approximation with ACT undershoots the small features in the eastern part of the region, which are indeed due to technical distortions.
